Big O Notation

The Big O Notation is a mathematical, asymptotic notation that describes time complexity and space complexity of algorithms/ function when the argument tends towards a particular value of infinity.
For example, O(n) might be the same complexity of an algorithm that traverses thought an array of length n,
similarly, O(n+m) might be the time complexity of an algorithm that traverses through an array of length n and through a string of length m.
The following are examples of common complexities and their Big O notations, ordered from fastest to slowest

• Constant: O(1)
• Logarithmic: O(log(n))
• Linear: O(n)
• Log-linear: O(n log(n))
• Quadratic: O(n²)
• Factorial: O(n!)

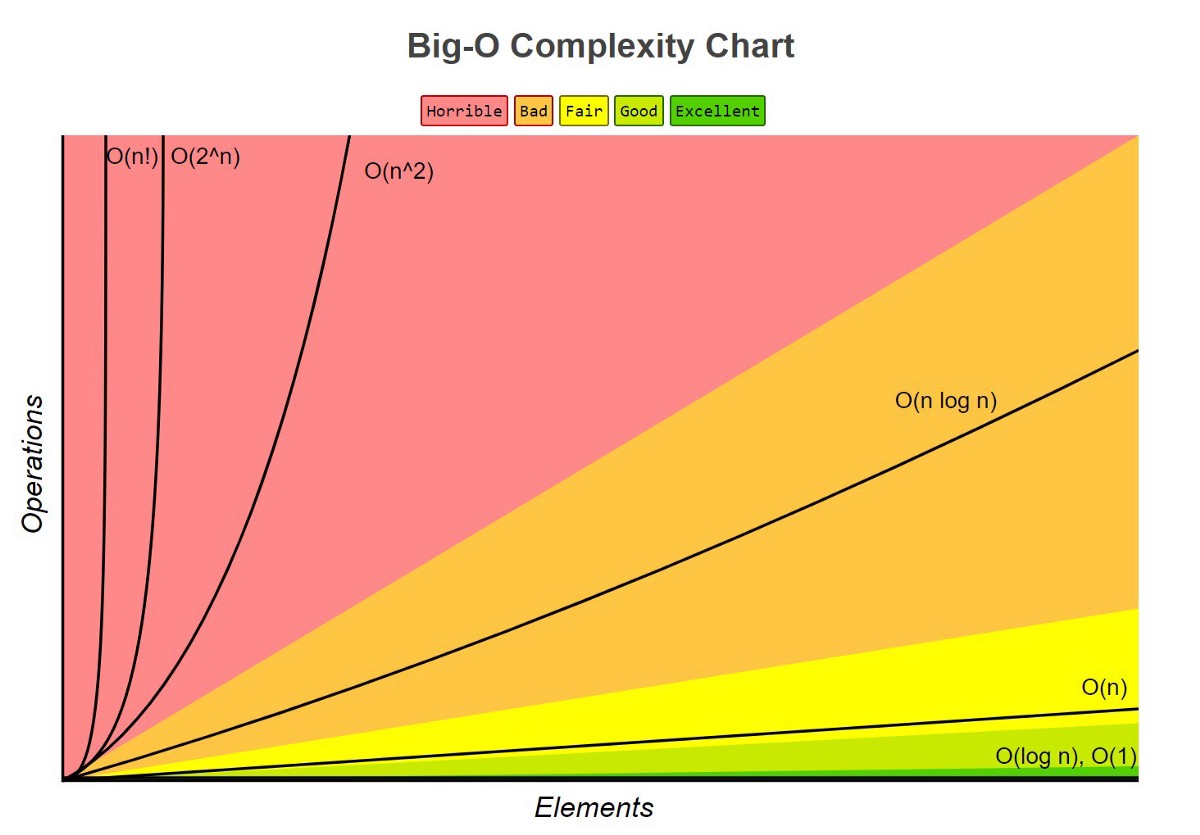
Sometimes there may be best/ average/ worst case scenario depends on the input data, how they’re structured and so on, so in other words depend on algorithm (quick sort for example) but Big O usually refers to worst case scenario.

Examples of algorithms and their time complexity:

• fun(arr[]) ⇒ 1 + arr[0] we just return static number and first element of an array (assume that’s not empty), so the size of input data will not affect the complexity anyhow. the time complexity will be O(1), in other words constant.
• fun(arr []) ⇒ sum(arr) here we are summing the given array, so we have to traverse through whole array, in other words the more elements are in given array, the more work our algorithm need to perform, so its linear complexity, in other words O(n).
• fun(arr []) ⇒ pair(arr) here we are pairing all elements, assume that it’s done by nested for loops. Then guess what, it would require going through every element twice. In previous example it was O(n) to iterate over given array. In this case it will be O(n²).

The constants in Big O Notation does not matter and how to simplify it.

Let’s assume that we have function that do bunch of elementary operations, it sums up few numbers, declare some variables, an array with few elements, it’s going to be algorithm that may run in O(25) but that would be written down to O(1). So you never want to say O(25) as it does not really make sense, and you should write it as O(1). The second example might be an algorithm in which we iterate over a given array from left to right and from right to left. That would be an O(2n) complexity, but you would drop a two because that’s a constant, so it would be just O(n). Also, important thing to remember, let’s assume that in our function we have a pairing algorithm and the one described just before. That is O(n² + 2n) but we would remove the two as its constant and n also as it’s become meaningless next to the N squared, so it would be O(n²).

Other example: O(n! + n³ + log(n) + 3) ⇒ O(n!) as factorial would growth the fastest. We were able to drop this in above way as we were iterating on the same input data N. Now assume that we do the same but for input we’re going to get two different arrays of size M and N.

O(m² + 2n) can we transform it to O(m²)? No! We can not! As those are different inputs, so we want to know the behaviour as it relates to these two different inputs, and you can imagine that there is actually a scenario where m² is tiny compared to N.
Imagine M is equal to two and N is equal to a thousand, then m² would be smaller than N. That’s why when you have two variables, you do always want to keep both of them. So it has to remain O(m²+ n)(we can still drop constants)