Trees

a data structure that is constructed with nodes, where each has some value and may point to child-nodes, which recursively form subtrees in the tree.

The first node in a tree is called a root, some nodes on the bottom of the tree may not have child-nodes, and they are referred to as a leaf-nodes or just leaves.
The height of a tree is the length of its longest branch. Branches are paths between root, and it leaves.
The depth of a tree node is a distance from its tree’s root, it’s also known as a node’s level in the tree.

A tree is basically a graph that’s connected, directed and acyclic, that has an explicit root node, and whose nodes all have a single parent (except a root node which hasn’t parent). You may find out more about graphs here In most of the implementations nodes does not have a pointer to their parent, but they can if it’s desired.

There are many types of trees, like binary trees, heaps, AVL and more.

• Binary Tree

A tree whose elements have at most two children nodes.

The structure of a binary tree is such that many of its operations have a logarithmic time complexity, making the binary tree an incredibly attractive and commonly used data structure. Why its usually logarithmic complexity, because whenever we choose one of child-node we reject the second half.

Read more about logarithms here.

• K-ary Tree

A tree whose nodes have up to k child-nodes. A binary tree is a k-ary tree where k==2.

• Complete Binary Tree

A Binary Tree that’s almost perfect. It’s a tree in which all the levels are completely filled except possibly the lowest one, which is filled from the left. A complete binary tree is just like a full binary tree, but with two major differences. All the leaf elements must lean towards the left.

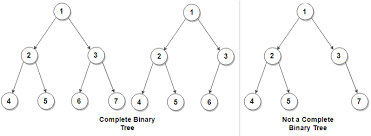
• Perfect Binary Tree

A Binary Tree whose interior nodes all have two child-nodes whose leaf nodes all have the same depth. Example:

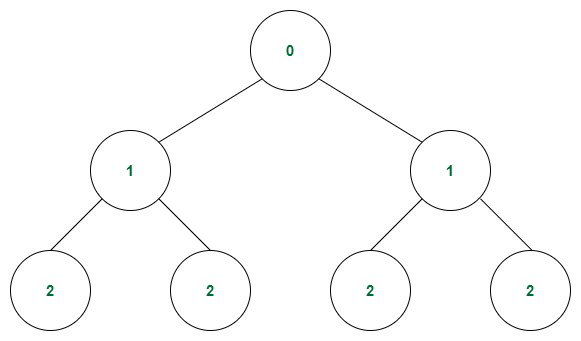
• Balanced Binary Tree

A Binary Tree whose nodes all have left and right subtrees whose heights differ by no more than 1.

A balanced binary tree is such that the logarithmic time complexity of its operations is maintained.

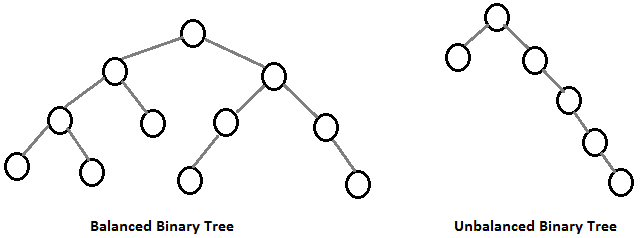
Inserting a node at the bottom of the following imbalanced binary tree right subtree would clearly not be a logarithmic time operation, since it would involve traversing through most tree nodes.

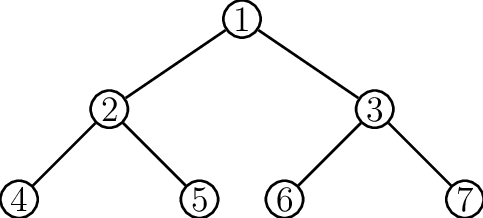
• Full Binary Tree

A Binary Tree whose nodes all have either two child-nodes or zero child-nodes.